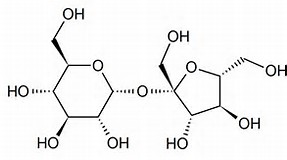
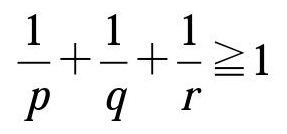秋が深まり、理系の皆さんは理科の追い込みにも力を入れていることでしょう。化学は数学に比べ、安定した得点を見込める科目でもあります。なかでも有機分野は暗記メインの無機分野に次いで短期間での攻略が可能です。脂肪族、芳香族についての知識を整理した上で(とくに私大、センターの有機分野ではここの部分の知識差が点差につながる)、難関入試のハイライトである構造決定問題の訓練をしていくことになります。ここで大事なのは、異性体(構造、立体)を把握することです。分子式は同じで性質が異なるものを異性体といいますが、構造異性体に関してはまず「不飽和度U」、「C骨格での分類」、そして「官能基での分類および、位置」の順で抜け目なく調べることです。パターンを確立しておかないとミスが起きやすくなり、ただ闇雲と数をこなしていっても得点には結びつきません。高分子分野については手薄なまま受験に望む生徒がなぜか多いのですが、糖類・アミノ酸・タンパク質を筆頭に直前に力をいれて他の受験生とすぐに差をつけられる「おいしい」暗記分野です。直前期に復習しやすいよう、いまのうちからまとめておくことをオススメします。
カテゴリー: 未分類
物理も作図が大事
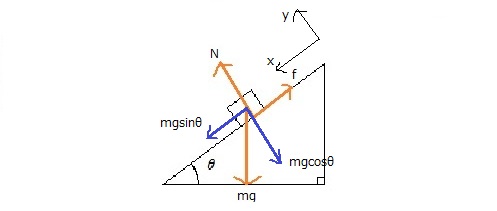
以前、数学では作図することが大事だという話をしました。それは物理にも言えることです。特に、高校1年生のみなさんは中間テストの範囲に運動の法則が含まれている人も多いのではないでしょうか。力学では①作図をする、②力を図示する、③2方向に力を分解する、④つりあいの式や運動方程式を立てる、という4ステップで解くのが基本です。これを正確に行うために、作図をしっかりとやることが重要です。
作図は問題を正答するための第一歩であるということを覚えておいてください。
二次試験の問題に挑戦
10月になり、いよいよセンター試験まで100日を切りました。いよいよ受験勉強も佳境の時期です。今日授業をした生徒も、大学の二次試験の問題に取り組みました。しかし、初めて向き合う二次試験の問題はなかなか難しく、苦戦していたようです。
この時期は二次試験の問題にはまだまだ歯が立たないという人が多いと思います。しかし、根気強く取り組むことで二次試験の解き方の感覚がつかめるようになっていくものです。受験の日はどんどん迫ってきますが、焦らずに積み重ねていってください。
授業をする中で感じたこと
今日は小学5年生の算数の授業を2つ担当しました。高校生を教えるときとはまた違う雰囲気でした。高校生を教えるときは厳密さ、論理性、問題のテクニックなどをメインに説明し、雑談も少なめです。今日の授業では身近な例を出し、おしゃべりしながら楽しく教えることで退屈させること無く授業ができ、「楽しくて分かりやすかった」とフィードバックがもらえました。雑談が少なめの高校生の授業でも「楽しい」との感想を得られるような授業をするために、雑談と説明のバランスを見直していきたいと感じました。
「勉強する意味はあるの?」
先日、生徒から「数学の勉強をして何になるのか。将来役に立たなくないか?」と言われてしまいました。
理系はまだ計算問題などで利用することがあるため絶対に無意味だと言う人はいないでしょうが、文系の人は試験以外で使うことは少ない為「数学の勉強は自分の将来のために必要じゃない」と言う人もいます。
もともと数学が嫌いでそう言っているのかもしれません。
数学の先生に同じことを質問すると「社会の~~で役に立っている」という例を上げてくれる先生もいらっしゃるかもしれません。社会で役に立っているから勉強しなくちゃいけない…。と言うのは腑に落ちませんね。
しかし、よくよく考えてみてください。
今の自分には確かに数学を利用した何かをすることはないにしても、何年、何十年先の自分はどうでしょうか。もしかしたら、何気ない場面で数学の知識が必要になるかもしれません。
将来、自分がどういうふうに転ぶかなんて分からないのです。
ただ授業時間を苦痛に思ってやり過ごすよりも、今しかできない勉強に力を入れてみてください。きっといつか身を助けます。
これは他の教科にも当てはまることです。
将来なんてわからないですし、授業は出なければいけません。そうならば、寝て過ごすなんて勿体無いことをせずに、真剣に先生の話に耳を傾けてみてはいかがでしょうか。
新しい発見があるかもしれませんよ。
整数問題への取り組み
整数問題は受験生が苦手とする分野の1つです。ほかの分野に比べて、解法が漠然としていることが原因のひとつかもしれません。難関国立大の入試において難しすぎて差がつかないような整数の出題がみられることもありますが、基本的な問題にはいくつかのパターンがあります。まずは、このレベルを確実にできるようにしておくことが重要です。整数問題の解法が漠然としているとは言っても、ゴールはどの問題も同じで、「範囲(幅)を絞る」ことです。例えば、整数pが1以上√5以下と分かれば、pの候補は1と2と分かるでしょう。この範囲(幅)の絞り方が問題の形によって変わっていくだけなのです。参考書や問題集で基本、標準問題の解答解説を読みこんで、その手法を真似ていくと習得は早いです。どの分野にもいえることですが、苦手分野であっても足を引っ張らないようにしておくことが難関突破の最低条件です。手を抜かずに頑張りましょう。
思い立ったが吉日
段々と秋が深まってきましたね。特に高校・中学3年生の皆さんは、「勉学の秋」とすることができているでしょうか。そろそろ成績が気になり始める時期にも差し掛かるので、今回は僕の実体験も交えた、勉強法の紹介をします。
僕も去年の今頃は、模試の成績とにらめっこしていた覚えがあります。なかなか成績が上がらず、周りとの差に焦りを感じ、とにかく問題を解こう、と過去問はひたすら解いていました。
それも大事なことかもしれません。しかし、帰ってきた模試の答案・解説を見てみると、かなり簡単な所で点数を落としていることが多かったんです。例えば、数学で使う公式の符号を間違えていた、古文の単語の意味を間違えてストーリーが全然違った、問題指示を見ていなかった・・・などです。それから、一度自分を見つめ直して、公式、単語、文法など基礎基本を勉強しました。すると、ミスで点数を落とさなくなっただけでなく、解けなかった問題に手が届くようになり、安定した成績をとることができるようになりました。なにより、自分に自信が持てるようになったことが大きかったと思います。
今一度、自分の頭の中を整理してみてください。僕のようなイージーミスで点を落としている人、あやふやにしている単語や文法がある人、いませんか。今、この時が、復習のラストチャンスかもしれませんよ。
思い立ったが吉日、です。
なぜ1は素数じゃないのか。
生徒に「素数ってなにかわかる?」と聞いてみたところ、「1とか2とか3とか5とか!」という風に返されてしまいました。
確かに2,3,5は素数です。ただし、1は素数に含まれないのです。
「28を素因数分解してごらん」というと「2x2x7」と答えてくれました。
感覚では1が素数でないことを理解してはいるようです。
さて素数については以前も紹介しましたが「1とその数自身でしか割れない数」のことです。
素数ってなにがある?と聞くと1を答えてしまう人は思いのほかいます。
ではなぜ1は素数に含まれないのでしょうか。
それは1を素数に含んでしまうと困ったことが起きます。
1を素数だと考えて28を素因数分解してみましょう。
28=1x2x2x7
28=1x1x1x1x2x2x7
28=1x1x1x1x1x2x2x7
1はどんな数に掛けても影響を及ぼしません(元の数は変わりません)。1を素数に含めると素因数分解の書き方が無限に出てしまいます。
これは「素因数分解の一意性(数は一通りの素数の積で表せる。)」というルールに反します。
この素因数分解の一意性を守るためにも1は素数に含まない。ということになりました。
エラトステネスの篩を知っている人は、1が素数の場合の篩を考えてみると更に理解が深まるかもしれませんね。(素数が1しかない!という事件が起きます。)
用語の定義理解の大切さ
みなさんは例えば電界や電位という言葉を聞いて、すぐに周りに自分の言葉で説明することができるでしょうか? 教科書の説明をそのまま暗唱できたらOKではなく、たとえば「電界の強さとは何か?」と聞かれたら、「ある場所にプラス1クーロンの電荷を置いて、それが受ける電気的な力」というようになるべく自分の言葉で説明して欲しいのです。物理学習では分野ごとに様々な用語が出てきますが、物理が不得意という生徒たちほど、これらの用語の定義をあいまいのままにしていることが多いです。用語を確実におさえるということは、物理現象を捉えるということに繋がるので早い段階からこのことを意識しておいたほうがいいでしよう。基本を疎かにすることのないように。
数に隠れた魅力
学校の最寄り駅まで300円……そこから歩いて10分……帰りは買い物でいくら使う……21時までには帰りたい。明日は用事があるから6時には起きよう。
日常の中で数というのは無意識のうちにそばにあります。普段何気なく使っている数でも隠れた魅力があるものです。
例えば「6」。6は完全数でありながら、高度合成数でもあります。
完全数?高度合成数?と思った人もいると思います。なにやらかっこいい名前ですが難しいことはありません。
完全数とは「それ自身を除く約数の和がその数自身と等しい自然数」のことです。
6で考えてみます。6の約数は「1,2,3,6」自身を除くので1,2,3の和を求めます。
1+2+3=6
見事に6の約数(それ自身は除いてますが)の和は6になりましたね。
完全数は他に28や496などがあります。
次に高度合成数とは「それ未満のどの自然数よりも約数の個数が多い自然数」のことを指します。
また6について考えてみます。6未満の数のそれぞれの約数1は1つ、素数である2,3,5は当然2つ、4は3つ(1と2と4)です。そして6の約数は1,2,3,6の4個です。
6未満の5個の数のどの約数の数よりも大きいですね。
高度完全数は他に1,2,4,6,12,24,36などがあります。約数の個数の求め方をすでに習っている人は探してみても面白いかもしれませんね。
今回は「完全数」「高度合成数」を紹介しましたが他にも「カプレカ数」や「調和数」,「タクシー数」などなど素敵な数がたくさんあります。