「フィボナッチ数列」「黄金比」という言葉を耳にしたことはありますか?
まず、フィボナッチ数列とは前の二つの数字の和を並べた数列(1,1,2,3,5,8……)のことです。フィボナッチという名前はイタリアの数学者レオナルド・フィボナッチにちなんでつけられたものです。
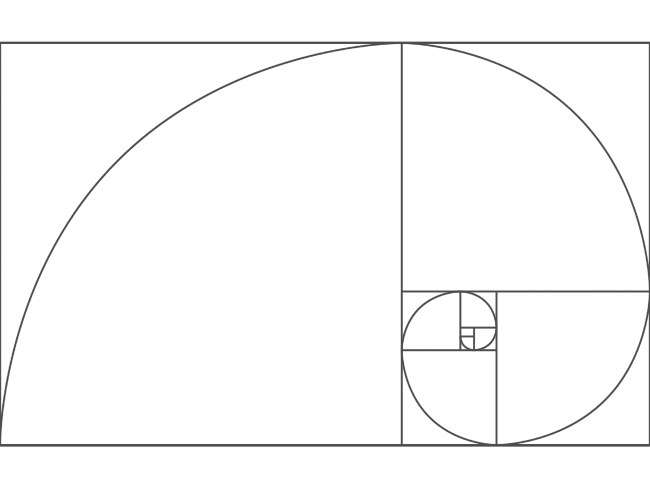
次に、黄金比について説明します。黄金比とは近似値1:1.618(約5:8)の比のことで、最も美しい比だといわれています。
黄金比の特徴は「黄金比の長方形について。短い方の辺を基準として正方形を作り二つに分けた時、長方形の図形の辺の比がまた黄金比になる」ということです。とても不思議な比です。
さて「フィボナッチ数列」と「黄金比」一見なんの関係性もなさそうに見えます。
しかし、フィボナッチ数列の連続する項の比率を計算する(二つの数を選び、小さい方の数で大きい方の数を割る)と面白いことが起こります。
フィボナッチ数列(1,1,2,3,5,8,13,21,34,55……)
1/1=1
2/1=2
3/2=1.5
5/3=1.6666……
8/5=1.6
13/8=1.625
21/13=1.61538……
そろそろわかってきましたか?フィボナッチ数列の連続する項の比率は黄金比に近づきます。
一見関係なさそうに見えるものがこんなところで繋がっているところに意外性と面白さを感じませんか?
もう既に数列を習っているという人はフィボナッチ数列の一般式を求めてみるのもいいかもしれません。