センター国語において、知識のポイントで多くの答えを絞ることができて比較的手間がかからないのが古文と漢文ですが、最もそれが顕著なのが漢文です。そして漢文において「知識」というのは、ズバリ、句形のことを指します。センターに出る(解答の決め手になる)句形というのはほぼ決まっていて、使役、受身、疑問、反語、否定、比較、抑揚、限定、詠嘆の形さえ押さえておけば後は過去問で演習を重ねるだけで高得点(15分以内で8割から満点)が期待できます。学習上のポイントとしては、句形の勉強をダラダラとやらないことです。漢字の書き取りの勉強をするわけではないので、基本的には目で見て慣れて覚えるだけで大丈夫です。ほとんど勉強したことがなくても、3時間ほどで上記の句形をすべて網羅できるはずです。その後、知識のブラッシュアップを兼ねて過去問演習にとりかかりましょう。短期間での攻略が可能なセンター漢文。国語が苦手だという理系の生徒であっても、ここで手を抜いてしまうのはもったいないです。1点でも多く、点数をもぎ取っていきましょう。
月: 2017年10月
宿題について
今日は小学5年生の算数の授業をしました。50分という限られた時間の中で解説できる問題はとても少ないです。宿題をするときは、ただ解くだけではなく、模範解答を大いに活用しましょう。答えを見ることに引け目を感じる必要は全くありません。解答を確認して分からないところを明確にして授業にのぞむ習慣をつけましょう。自分がどこで詰まったのか、どこまでは分かったのかを説明できるようになると成績は格段にアップするでしょう。
2次試験を見据えたセンター対策
センター試験まで三か月を切っています。センターの配点が大きい大学を志望する生徒はこれからはセンター型の勉強へと切り替えていかなければなりませんが、そうでない人もこれを機にセンター試験の過去問や予備校各社から出ている予想問題集にあたってみて欲しいです。センター試験は基本・標準問題の宝庫で、全範囲を網羅した出題をしてきます。よって、過去問や予想問題集で勉強することで高校の学習範囲を効率良く演習・復習できるのです。そして、このレベルを確実にしておくことが2次試験突破のキーになります。最難関レベルの大学を除けば、近年は2次で求められる学力はセンターレベルと大差があるわけではありません(体感的な難易差は、形式の違いによることが大きいです)。特に現役生はセンター試験前に2次力を完成させることは時間的に難しいので、センタ―試験への準備をしていくなかで2次試験への備えをしていくと効率が良いです。解答、解説をしっかりと読み込み、2次試験でどう活かしていくかを考えながら取り組むといいですよ。
英語長文問題への取り組み
低学年より頑張ってきた文法、構文の勉強を基礎にして受験生の皆さんは日々長文問題に取り組んでいることでしょう。長文問題(主に論説系)において得点力を上げるためには、英文の論理関係を追うことです。抽象から具体へと論の展開がなされていることをしっかりと意識して、「対比」、「具体例」、「言い換え」、「追加」、「因果」を表すディスコースマーカーを見逃さないことが内容把握に欠かせません。日々の演習で意識していきましょう。センター試験の最後の大問の英文は論理展開が「かなり」明快で英文レベルも標準的なので、過去問10回分ほどを解いてみるとかなりいい勉強になりますよ。単語、熟語はスキマ時間をうまく使って覚えていきましょうね。
高校生の計算力アップについて
計算力をあげたいと思っても、なかなか日々の学校生活のなかで計算練習だけに時間を割くことは厳しいですよね。しかし計算力は理系科目において必須の能力です。ケアレスミスの主因であることも考えると計算力不足は死活問題であると思います。そこでおススメするのは、数学の参考書や問題集の解答解説の計算部分を自力で最後までやり抜くことです。解き方だけが分かればいいやと解説中の計算式を眺めて終わりにするのではなく、実際に手を動かして解いてみるのです。数学の教科書や参考書、問題集の解説を読む機会は皆さんかなり多いはずです。解答を眺めるだけではなく、計算部分だけは自力でやっていくようにすると計算力アップだけではなく、問題の解法まで記憶に残りやすいので一石二鳥ですよ。このとき、1度やったことのある問題であっても大丈夫です。受験は時間と勉強量のせめぎあいです。効率よく勉強を進めていきましょう。
なぜ黒板につけた磁石は落ちない?
黒板に張り付いた磁石がなぜ落ちてこないのか、ということを考えてみたことがありますか?高校1年生のみなさんは、最近静止摩擦力について習ったと思います。F=μNの式で最大静止摩擦力の公式が与えられるように、摩擦には垂直抗力が関係しています。磁石は磁力で黒板と引き合って垂直抗力が増すので、その分最大静止摩擦力が大きくなり、摩擦が重力とつりあって黒板にくっつくのです。
このように、物理を勉強していくと日常の色々なことが説明できるようになります。みなさんも、ぜひ身の回りの「なぜ?どうして?」を探してみてくださいね。
生徒に合わせた授業を
オンライン家庭教師ではさまざまな学力の生徒を受け持っています。受験対策、学習のペースメーカーとして、他塾の難しい問題の解説、学校の授業の予習復習として、生徒の目的も一人ひとり違います。手間暇かかることですが、教材選び、解説の方法、授業の構成をできるだけ生徒の目的に合わせて授業しています。生徒の変化に気づき、フォローするために授業の合間にコミュニケーションとることも私たちの重要な仕事であると感じました。
コンピュータさん13は素数ですか?
ある時突然、「13は素数ですか?」と質問されたとします。きっと皆さんはすぐに「素数です」と答えることができるでしょう。
それは13が素数であるということを元から知っていたからかもしれませんし、13以下の素数「2,3,5,7,11」で13が割り切れないと瞬時に考えたからかもしれません。
では、コンピュータに「13は素数?」と質問してみたときのコンピュータの考え方を紹介します。
コンピュータは素数の定義のみを知っているとします。(2や3が素数ということは教えていません)
私達なら13以下の素数のみ割り算を行えば良いとわかりますが、そもそもコンピュータは13以下の素数が何なのか分かっていないのでそれは不可能です。
では、どういう動きになるのでしょうか?
それは、1から順に12まで割って行こうとします。
つまり……「13/1…13/2…13/3………13/12」というふうになります。
非効率的だと感じませんか?
ではここで2つアドバイスを上げましょう。もちろん「13以下の素数で割る」というのは不可能です。
与えるアドバイスは「13の平方根以下の自然数で順に割っていく」「2以上の自然数のみ考える。」の2つです。
少し複雑でしょうか?
具体的に考えてみましょう。13の平方根は3.6…..ですので、「13の平方根以下の自然数」とは「1,2,3」となります。
さらに、「2以上の自然数のみ」ということになるので、2つのアドバイスにあった数は「2,3」のみになります。
つまり、2つのアドバイスを与えることでコンピュータは「13/2…13/3」を計算するだけで素数判定を行うことができるようになるのです。
たった2つ変えただけなのにかなりの手間が省けましたね。
なぜ13以下の平方根以下の自然数でいいのか?という疑問が浮かんだ人はいませんか?
それは平方数をこすと同じ数が出てくるからです。具体例をあげます(素数では難しいので18を用います)
18(平方根は大体4.2です)を二つの数の積で表していくと……「1×18,2×9,3×6」となります。4以上の数を考えると、既に出たものの順番を入れ替えただけになります。だから平方根以下の自然数のみ考えればよいのです。
実は、今回考えた手順の簡略化(計算の効率化)というのが「アルゴリズム研究」の基本的なものです。
アルゴリズムとは大雑把に言ってしまえばコンピュータを動かすための命令文のようなものです。これをいかに簡単にするか、というのがアルゴリズム研究です。
ちょっと方法を変えるだけでかなり効率的に素数を判定する事ができるようになりましたね。素数判定以外にも「最短経路問題」など身近なところに効率化を求めるようなものが有ります。気がついたときに少しだけ考えてみてはいかがでしょうか。数学の知恵が日常生活に役に立ってることを感じることができるのではないでしょうか。
有機化学をまとめる
秋が深まり、理系の皆さんは理科の追い込みにも力を入れていることでしょう。化学は数学に比べ、安定した得点を見込める科目でもあります。なかでも有機分野は暗記メインの無機分野に次いで短期間での攻略が可能です。脂肪族、芳香族についての知識を整理した上で(とくに私大、センターの有機分野ではここの部分の知識差が点差につながる)、難関入試のハイライトである構造決定問題の訓練をしていくことになります。ここで大事なのは、異性体(構造、立体)を把握することです。分子式は同じで性質が異なるものを異性体といいますが、構造異性体に関してはまず「不飽和度U」、「C骨格での分類」、そして「官能基での分類および、位置」の順で抜け目なく調べることです。パターンを確立しておかないとミスが起きやすくなり、ただ闇雲と数をこなしていっても得点には結びつきません。高分子分野については手薄なまま受験に望む生徒がなぜか多いのですが、糖類・アミノ酸・タンパク質を筆頭に直前に力をいれて他の受験生とすぐに差をつけられる「おいしい」暗記分野です。直前期に復習しやすいよう、いまのうちからまとめておくことをオススメします。
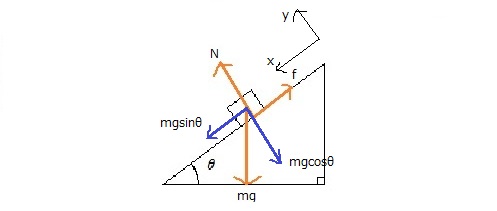
物理も作図が大事
以前、数学では作図することが大事だという話をしました。それは物理にも言えることです。特に、高校1年生のみなさんは中間テストの範囲に運動の法則が含まれている人も多いのではないでしょうか。力学では①作図をする、②力を図示する、③2方向に力を分解する、④つりあいの式や運動方程式を立てる、という4ステップで解くのが基本です。これを正確に行うために、作図をしっかりとやることが重要です。
作図は問題を正答するための第一歩であるということを覚えておいてください。