筑紫修学館スタッフブログ｜福岡の学習塾・個別指導は筑紫修学館

【入試情報】得点率から見た公立高校入試の分析～数学編

2021/07/29
TOP新着

みなさん、こんにちは(^^)/
学習塾筑紫修学館のスタッフブログです！
本日もスタッフブログをご覧いただきありがとうございます。

先日、今年3月に実施された福岡県公立高校入試の得点率に関してこちらのブログに掲載しましたが、今回からは各教科の内容をより深く掘り下げて分析してみます。
まずは得点率が50%を下回った数学です。

数学の問題の作成基準についてはこのように発表されています。
「基礎的・基本的な知識や技能及び数学的な見方や考え方を活用して、問題を処理する能力を多面的にみる。内容については、学校の授業を大切にして着実に学習しておけば解決できるようなものとし、その解決に必要な直観力、論理的な思考力をみる。」
(福岡県教育委員会の発表より一部抜粋)

一見難しそうな問題でも、学校や学習塾での学習をしっかりとこなして力をつけていれば、解くことができる問題が作成されているのです！
やはり日頃の学習がいかに大事であるかを考えさせられますね。

それでは大問ごとに見ていきましょう。
大問1は「数と式」「関数」「図形」「資料の活用」などの基礎的・基本的な識及び技能に関する問題、よく小問集合といわれている問題です。
この大問はいかに失点しないようにするかが志望校合格の大きなカギです。
それなのに1問だけ得点率が40%を下回った問題が。
それは(9)の円の中にある図形の角の大きさを求める問題でした。円周角の定理や，三角形の内角と外角の性質を用いる問題だったため、ほかの問題と比べて少し複雑に見えたのかもしれませんね。

大問2はヒストグラムに関する問題が、大問3では文字式の利用に関する問題が出題されました。
どちらの大問でもある考えに関して自分の言葉で証明する問題が出題されましたが、大問3では久しく出題されていなかった文字式の証明ということもあり、得点率は30%となりました。
学校や塾の授業では間違いなく学習する内容なので、やはり過去によく出題されたかどうかではなく、普段の学習がいかに大事かを考えさせられますね。

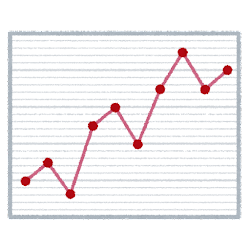
大問4では1次関数に関する問題が出題されました。
全体の得点率が約30%と、点数がとりにくくなってきています。
(3)では、兄と妹の歩いた時間を１次関数の式を用いて表し，２つの直線の交点の座標から時刻を求める問題で、得点率は約10%でした。
このような問題では関数の式や表，グラフを適切に用いて，事象を考察し説明する学習が正解を導き出すために必要になってくるのです。その中でも事象を具体的な１次関数の式やグラフで表すことや，２直線の式を連立方程式として解くことで２直線の交点の座標が求められることを普段の学習の中で理解して，問題を解決するまでの流れを順序良く表現することが大切です。

大問5では平面図形、大問6では立体図形の問題が出題されました。
どちらも例年得点率は低く、大問5では30%を、大問6では20%を下回る結果となりました。

平面図形では図形の性質や合同や相似、図形が成り立つための様々な条件を、立体図形では図形についての基礎的な概念や基本的な性質を理解することが大切です。
そこから、自分で条件について証明したり、面積や比、体積を求めるなどの問題に取り組むことが大事です。
基本が身についていない状態で問題に取り組むのではなく、まずは必ず基本的な知識を普段の学習の中で身につけることから始めましょう。
特に図形の問題では毎年得点率が５％未満の問題が出されるので、そのような問題に時間をかけずに、ほかの問題で確実に得点できるようにすることも必要です。

数学は、ほかの教科と比べても難しいなと思うことが多い教科ですが、普段の学習をしっかりこなしていれば解ける問題が出されていますので、これから受験を迎える皆さんはぜひとも、日々の学習を大切にしていきましょう！

次回は英語について分析を行います。
お楽しみに

筑紫修学館各校舎の紹介・お問い合わせはコチラ↓↓↓