みなさんこんにちは！今日は中学数学の『ミスをしなくなる解き方』についてお伝えします！

毎年夏期講習では個々の苦手科目・単元の克服に力を入れているのですが、長住校では中学3年生の数学に関しては福岡県の『公立高校入試の頻出問題をできるようになる！』ということを課題としています。

特に力を入れているのは入試問題の 大問1 から 4 までの問題で、中でも多くの生徒が苦手としている 大問4 の1次関数の記述問題には特に力を入れて指導しています。

『数学なのに記述！？そんなん私が一番苦手なやつやん…』と言う生徒は少なくないです。

ですが、解き方のポイントをおさえていくだけで簡単に解けるようになります！

昨年、数学が5教科で一番苦手だったある生徒は、夏期講習のこの時期には『1次関数難しいです…』と言っていましたが、何度も繰り返しポイントを確認していくことによって次第に解けるようになり、入試本番でもばっちり解くことができ、5教科の中で数学が一番いい点数を取ることができました！

(1番苦手だった数学が、得意な科目より断然良い点数だったことにはさすがに私も驚きました…当の本人も驚いていました(笑)とても良く頑張ってくれた結果だと思います！)

そして、今年の生徒達も初めは『え…まったくわかりません。なにから書きはじめればいいんですか？』と言っていましたが、もうすでに『先生！書けました！これで合ってますよね！！』と言ってくるようになりましたよ(^o^)

ではここで本題に入ります。解き方のポイントをおさえるだけで解けるようになると言いましたが、せっかく解き方がわかっても計算ミスをしてしまっては意味がないですよね。

『こんなのただの計算ミスですよ…』という生徒は多いですが、その『ただの計算ミス』なんかで点数を落とすってもったいないですよね。

そこで、ミスをしなくなる解き方について少しだけご紹介します。(1次関数の解き方のポイントに関しては、ぜひ長住校に来て授業を受けてみてください！（＾－＾）)

計算ミスを減らすためには、『とにかく簡単に』解いていくことが大事です。

入試の大問4の1次関数(3)は、グラフの交点を求める問題です。つまり連立方程式で解くのですが、計算ミスを減らすポイントが3つあります。

①連立方程式を解くために連立方程式を解かない！

連立方程式を解くためには、2直線の式を求める必要があります。

その式の求め方には2通りあります。その1つが連立方程式です。

ただ、連立方程式はとても計算ミスが起きやすいのです！

連立方程式を解くために連立方程式を解いて…なんてしていると途中で計算ミスをして答えがおかしくなった！なんてことがよくあります。

1次関数が苦手な生徒ほど連立方程式で解こうとするのですが、絶対にそれはしないようにと言っています。

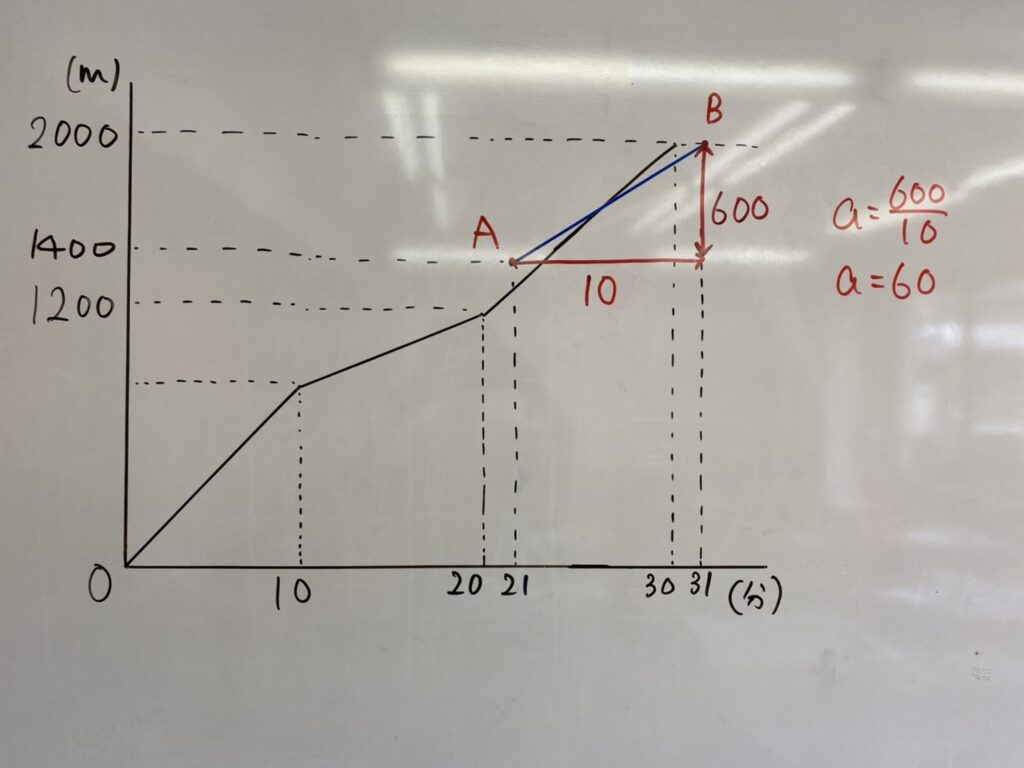
式を求めるときは、例えば点Aから点Bまで、右にどれだけ進んで上にどれだけ進んだかを考えれば傾きが求められます。簡単ですよね。

②無駄な移項はしない！

傾きが60とわかったので、1次関数の式y=ax+bのaに60を代入します。

y=60x+b　となりますね。

あとはbがわかればいいので、点Aもしくは点Bの座標をこの式に代入します。

例えば点Aの座標を代入すると、1400=60×21+b

計算して　1400=1260+b

ここからがポイントです！bを求めたい、つまりb=□のかたちにしなきゃ…と

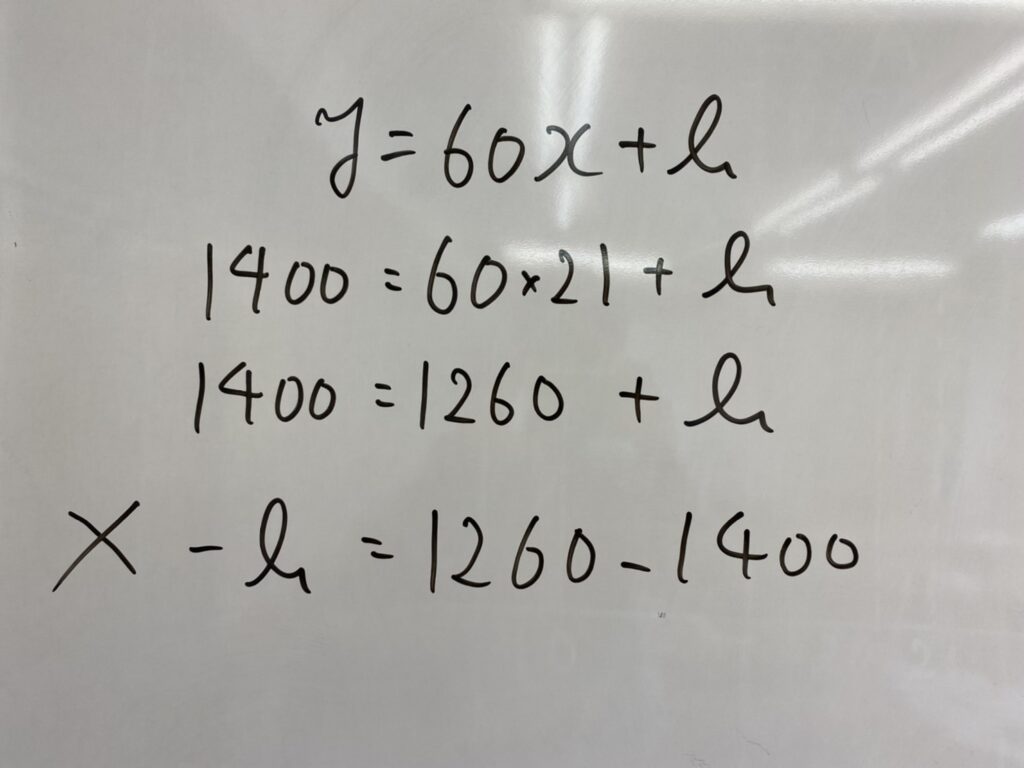
このようにbを移項してしまうと、bの前にマイナスがでてきてしまいます。1400も移項するときに符号がかわりますよね。

ここが符号ミスの大きなポイントです！こんなことはしなくていいんです！

b=□も□=bも同じなので、bはそのままで数字だけ移項すれば良いんです！

③自分が解きやすいように式をつくる！

2つの式が求められたら、あとは連立方程式を解きます。

1次関数の式はy=　のかたちになっているので代入法を使います。ここでも数学が苦手な生徒は代入法を避けて加減法で解きがちですが、代入法の方が絶対に楽に解けるので加減法は使わないようにしましょう。

ここで最後のポイントです！

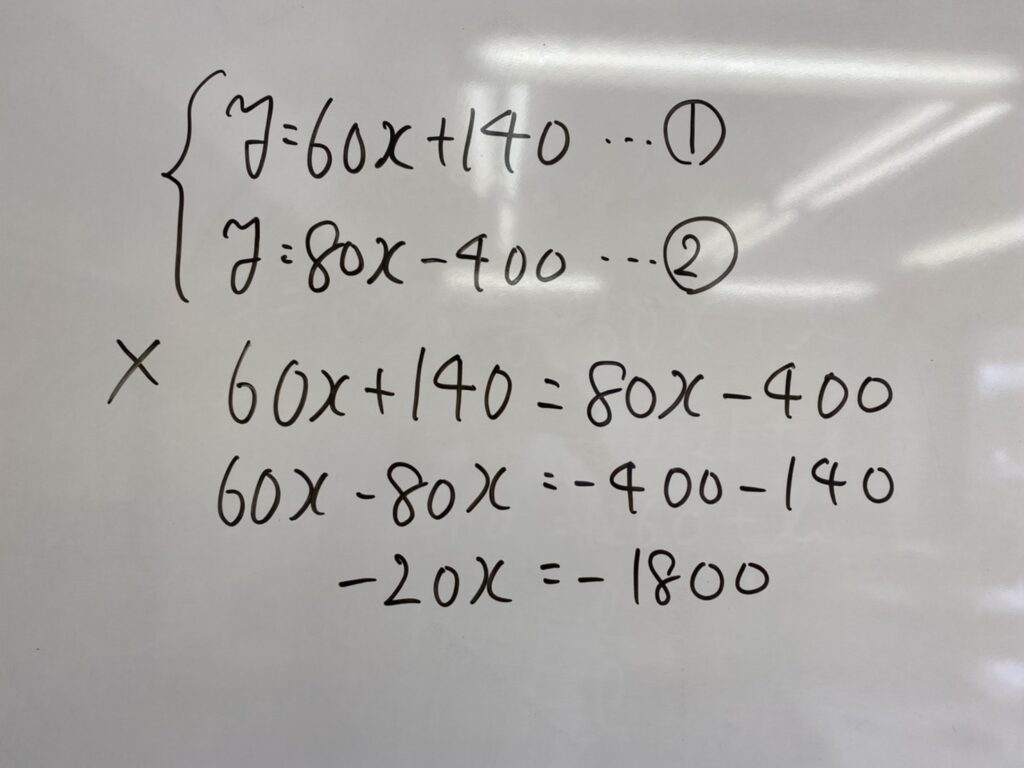
この場合の代入法は2つの式の右辺を=でつないでやればいいのですが、このように式をつくってしまうと計算した時にxの係数がマイナスになってしまいます。マイナスは計算の大敵ですよね。

ではこのように式をつくれば…xの係数がプラスになり、符号のミスが起きにくくなりますね！

このように、些細なことですが気をつけながら計算することで確実にミスをなくすことができます！

こんなことで？と思うかもしれませんが、こんなことで点数を落とさなくなるならやってみる価値がありますよね(^o^)

計算ミスが多い人はぜひ実践してみてください！

その他にもたくさん解き方のポイントがあるので、気になる方はぜひ筑紫修学館長住校にお越しください！！

LINEでお問い合わせ・ご相談

LINEでのお問い合わせも対応可能です。
細かなご相談もLINEでのご質問は最短翌日に回答いたします。

筑紫修学館 長住校 LINEアカウント

講座の案内、学習情報、お得なクーポン券などもLINEでお届けします！